第一部はプレス成形分野における機械特性についてご紹介しています。
横方向に拘束を加えた引張試験
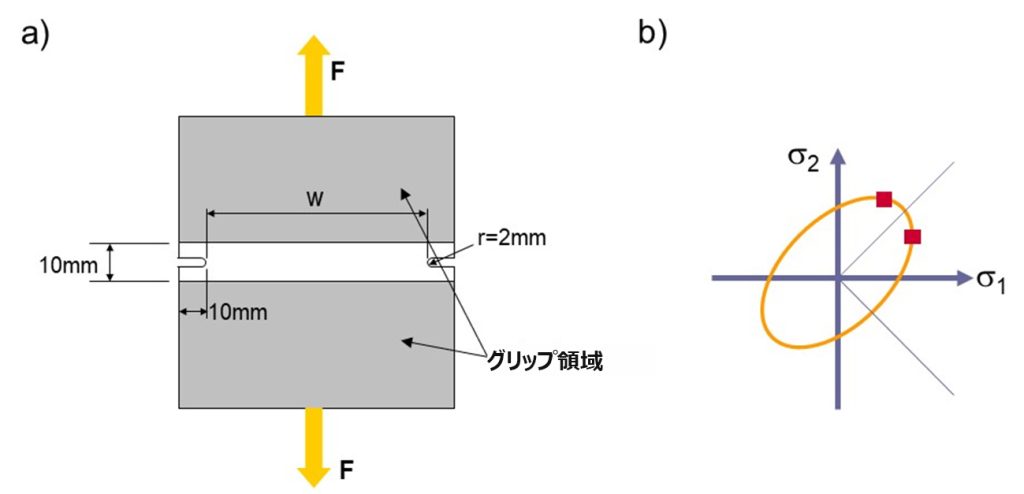
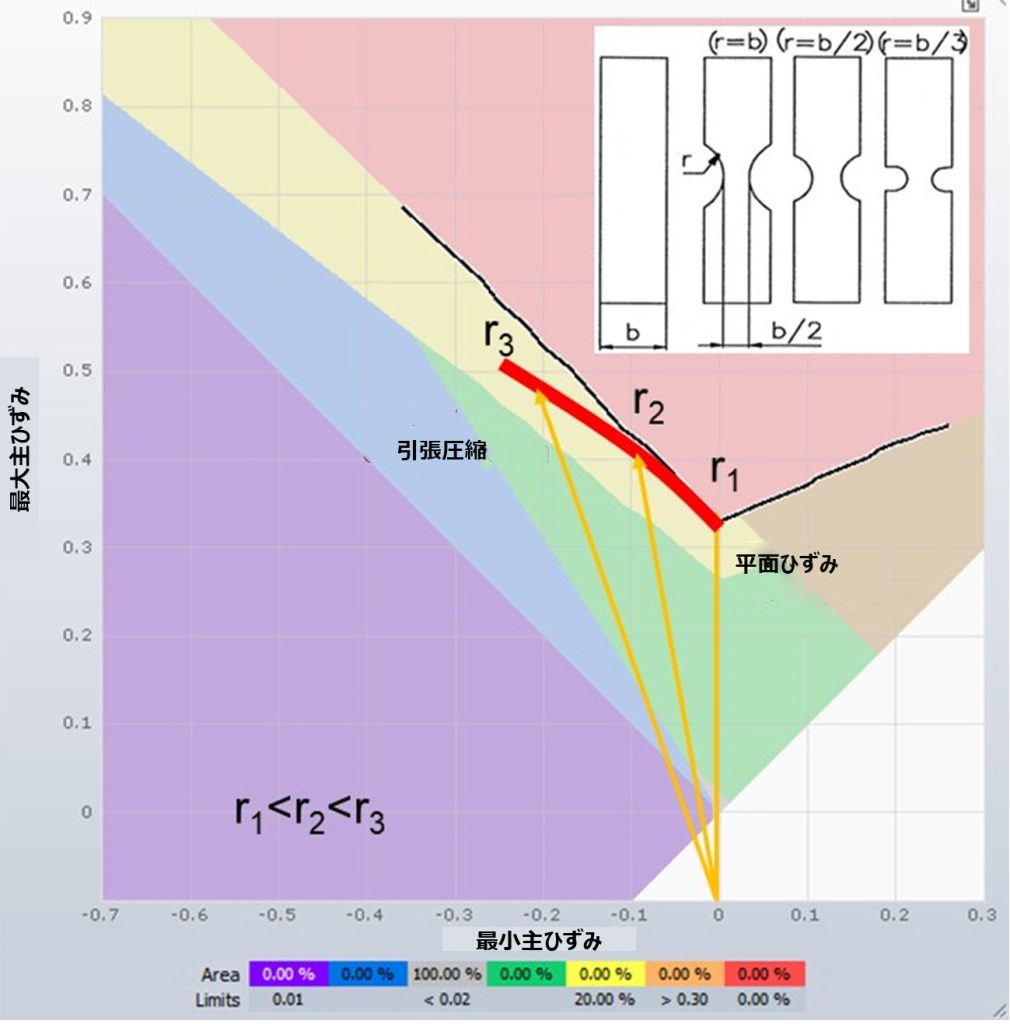
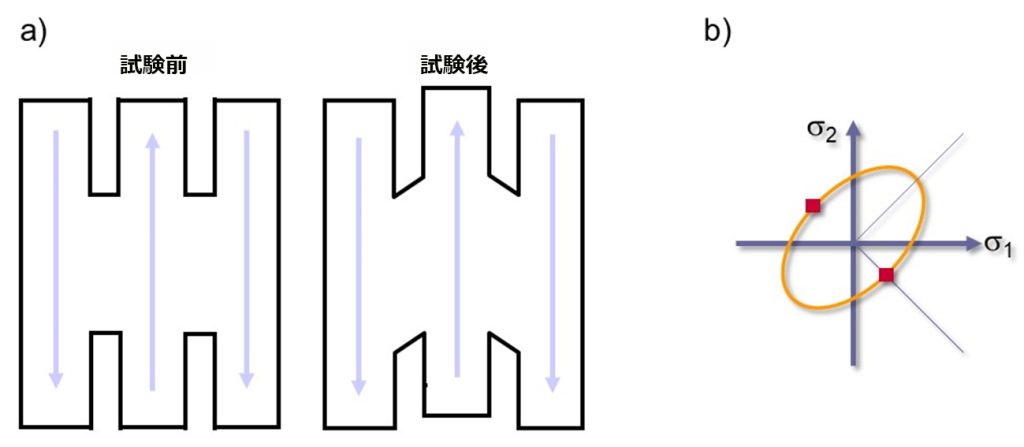
横方向に拘束を加えた引張試験(図10)を利用して、材料に平面ひずみ状態を発生させます。図11のとおり試験片の半径rを変更することで、横幅をある程度狭くできます。これで平面ひずみ領域だけでなく、FLDの圧縮領域の一部を網羅することが可能になります。この手法は1972年にRozzoおよびDelucaによって開発されました[5]。
図 10: a) 試験片の形状; b) 平面ひずみ状態から判定される降伏曲面上の位置。出典 [1]
図11: RozzoおよびDeluca[5]が開発したFLD左側の判定方法。出典: [1]
引張圧縮試験
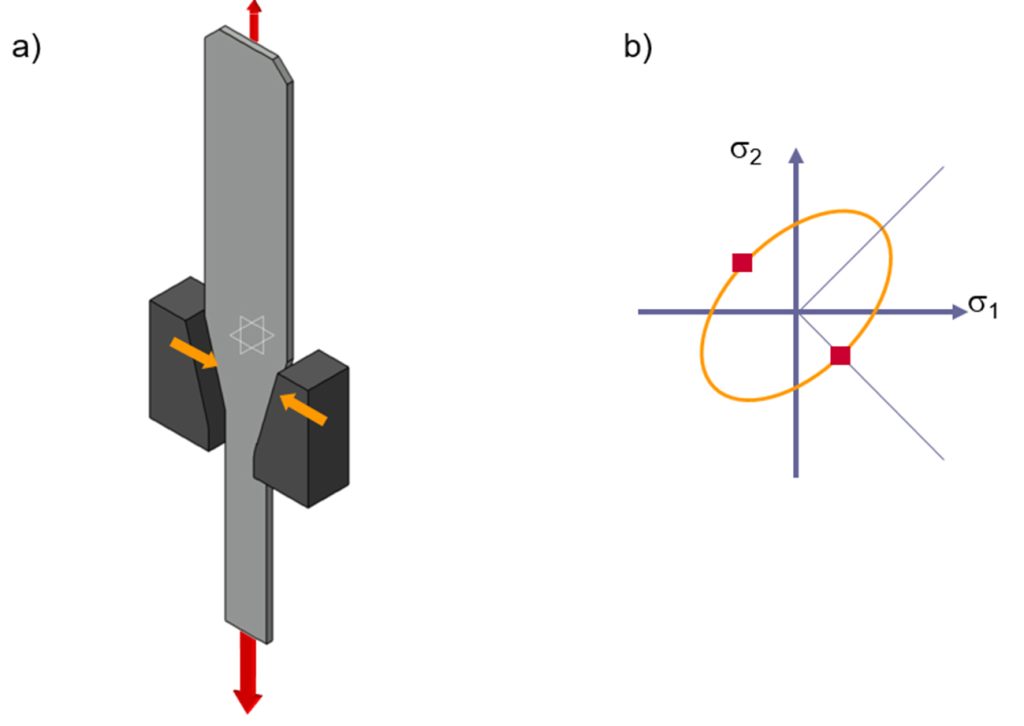
Sachs [6]がウェッジ試験とも称する引張圧縮試験(ドイツ語でKeilzug-Pruefverfahren nach Sachs)では、くさび部の横方向からの圧縮応力を一軸引張と重ねて適用します。可視塑性などの手法で変形を分析できます。
図12: a) 試験で使用するくさび状の材料片。b)試験で再現する降伏曲線上のポイント。出典: [1]
この試験では、深絞り加工におけるフランジ領域の応力圧縮状態を再現します。この試験ではくさび部の接触領域に生じる摩擦が結果に大きく影響するため、潤滑条件に非常に敏感であることが難点です。降伏曲面では、試験で再現されるポイントはせん断領域にあります(図 12-b)。
積層板の圧縮試験
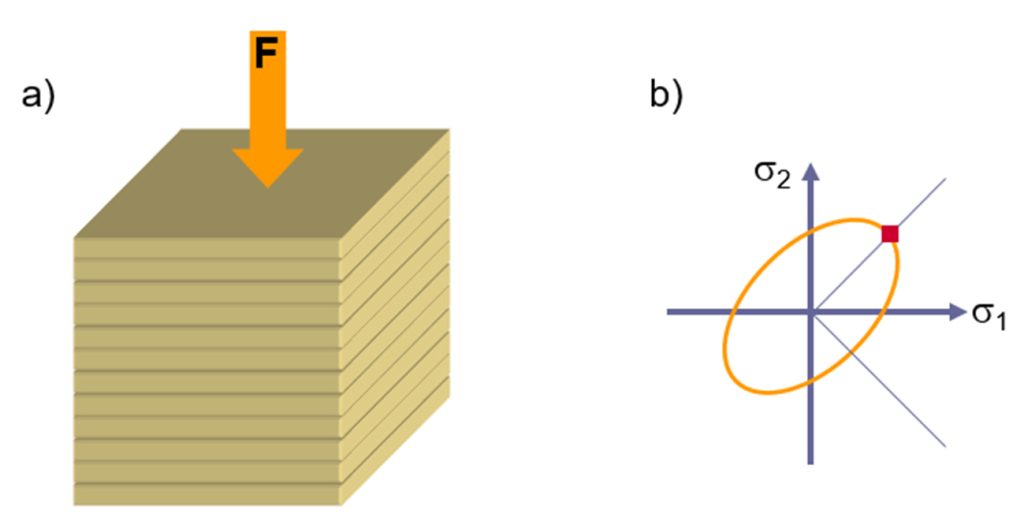
Pawelski [7]は積層板の試験片を用いた圧縮試験を初めて実施しました。積層板の圧縮試験は、DIN 50106 [8]の円筒圧縮試験を応用したものです。圧縮試験では材料は圧力下で収縮しないため、引張試験よりも比較的大きな変形が得られます。材料は薄板であるため、試験では複数の試験片を積み重ねますが、圧延方向に対して一様に配列する必要があります。そして摩擦の影響を減らすため、圧縮帯と試験片の界面にはテフロンシートを使用します。円周方向の変形は光学式変形測定器で記録します。また降伏応力は検出された変形荷重と理想的には円筒形とされる試験片の断面積から算出します。板厚方向の圧縮応力により、試験片は一様に膨張します(図13)。x方向とy方向の長さの増加は直交異方性に依存します。
図 13: a) 試験に使用する積層板の試験片。 b) 平面応力状態の特性試験で再現する降伏曲面上のポイント。出典:[1]
せん断試験
Brosius[9]に倣ったせん断試験は、薄板材料を最適な状態で単純にせん断するだけの試験です。この試験では、せん断応力下での流動抵抗を測定します。引張荷重と長さの変化は、試験装置の先端部分で計測します(図14)。せん断応力は可視塑性の変形解析から算出されます。
図14: a) 試験前後の試験片。b) せん断に特徴的な降伏曲面上のポイント。出典 [1]
バルジ試験
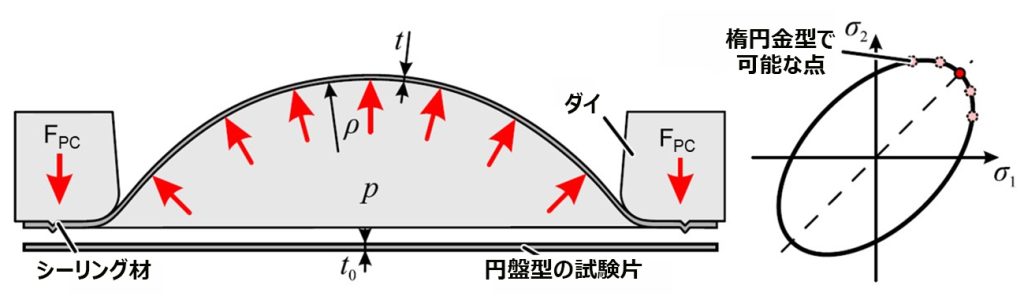
Hill [10] (1950)が開発した液圧バルジ試験は、真ひずみ約0.7までの降伏曲線を決定するもので、図15はその原理を示しています。しっかりと固定された円盤試験片の片側から液体を押し込むと、圧によって試験片は膨張し、最終的に頭頂で破断します。通常は液体(油または水性の媒体)、気体、粘塑性の媒体を使用します。媒体の圧力は圧力センサーで測定し、試験片の頭頂における薄板の半径と板厚は光学的または触覚的に測定します(図16)。
図 15: 液圧バルジ試験の原理と達しうる応力状態。出典: [1]
図16: 組み立てたバルジ試験の写真(出典: IFU Stuttgart)
NakajimaおよびMarciniak試験
前述のように、成形限界線図(FLD)の評価にはISO 12004 [2, 3]の規格があり、試験手順と評価方法が記載されています。この規格はFLD定義の平易化を目的としています。材料の特性評価には、例えば引張試験、バルジ試験、平面変形試験など、数多くの試験装置があるにもかかわらず、この規格では2種のパンチ、すなわちNakajima [11]による半球状のパンチとMarciniak [12]による平板状のパンチを備えた1つの伸び試験装置のみを規定しています。
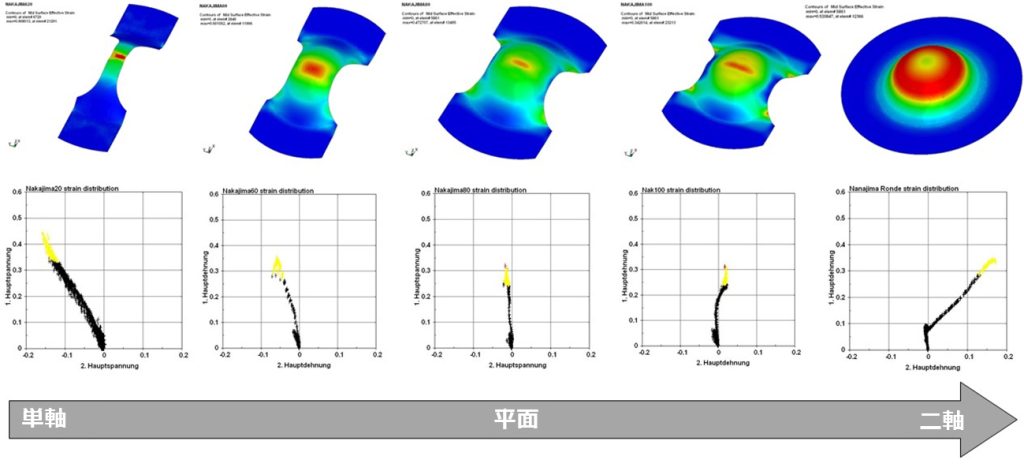
FLDの普遍的な定義を模索する中で、Nakajimaは独自の金型設定を用いて、複数の変形条件を分析するための試験用の設定を提案しました。いわゆるNakajima試験では、固定装置と半球状のパンチを使用します。試験片は複数の形状を用意することで、さまざまな変形形状を得ることができます。試験片のストリップ材は、形状全体の二軸条件から小さな幅の一軸応力まで、さまざまな変形履歴に応じて幅が異なります(図17)。
図 17: Nakajima試験における変形経路に対する試験片の影響。出典: [1]
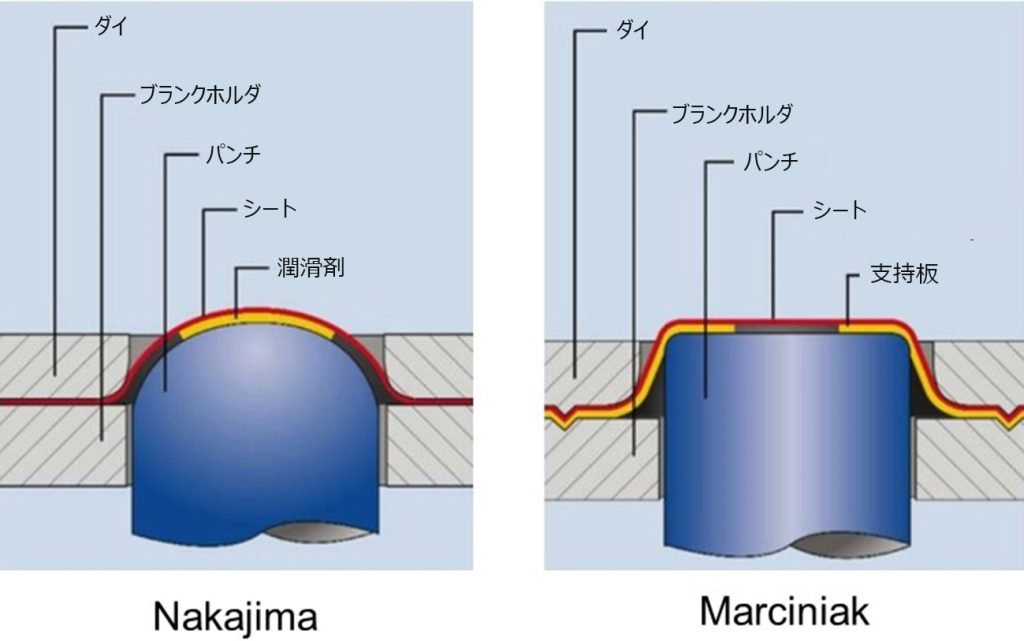
またFLCの最低ポイントに達する最も厳しい変形条件は、平面ひずみ条件と一致することも確認されました。MarciniakはNakajima試験と同様の機械構成を提案していますが、平板状のパンチを使用しています。シートと平板状パンチの間の接触条件が重要であるため、いわゆるMarciniak試験には、両方の接触面の間に支持板が必要です。これにより、変形の分布が均一になります(図18)。どちらの構成もDIN EN ISO 12004-2 [3]に準じています。
図18:NakajimaとMarciniakの金型形状は異なります。Marciniak試験では支持板を用いて平面変形を発生させることで、ディスクに平面領域が発生します。出典: Erichsen
十字型の試験片を用いた引張試験(二軸引張)
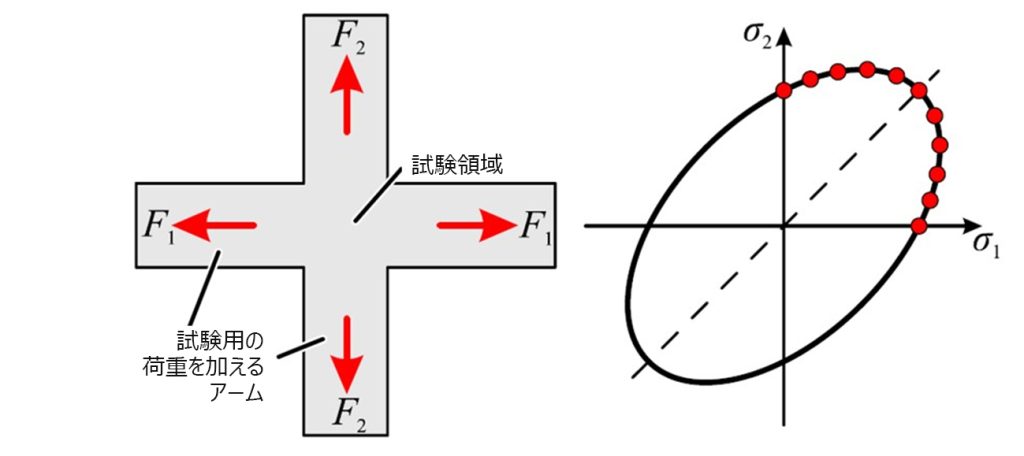
二軸引張試験では、十字型の板を2軸方向に引っ張ると、試験の中央領域に多軸応力状態が生じます。その原理と応力状態を図19に示します。
図 19: 十字型の試験片の原理と達しうる応力状態。出典: [1]
この試験では、どちらの負荷方向も荷重比を変えることができます。また流動応力の発展は降伏曲面の第一象限の中で開始します。この試験はISO 16842[13]に準じています。
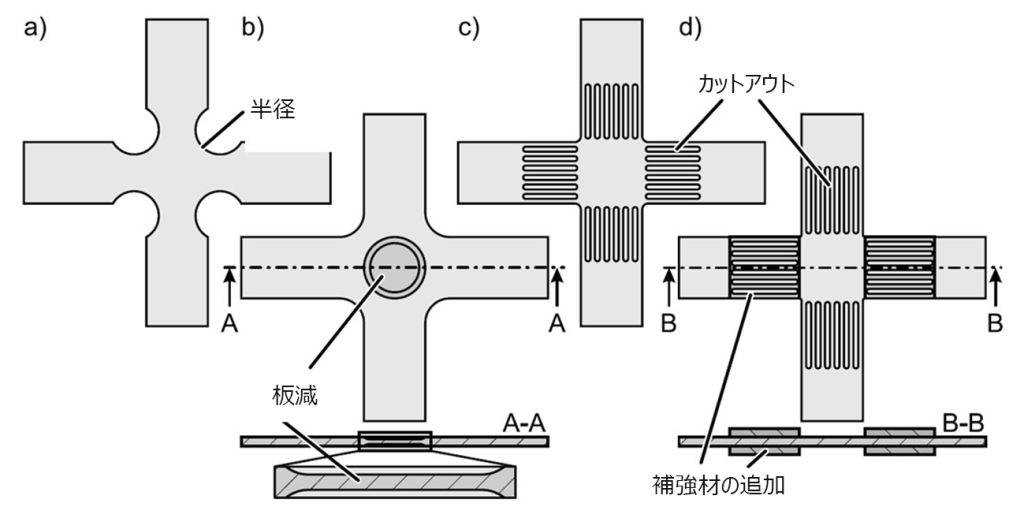
試験片に修正を加えなければ、わずかな塑性変形でも試験片の破損につながります。試験片の中心領域における応力状態と変形を均一に保つため、さまざまな形状の試験片が開発されています(図20)。
図 20: 二軸引張試験の調整 a) 半径のばらつき (Shiratori and Ikegami, 1967), b) 板減 (Wilson and White, 1971), c) アームの切り出し (Mönch and Galster, 1963), d) アームの補強 (Hou et al., 2021)
曲げ試験
たとえばISO 7438 [14]を用いて板金の曲げやすさを見極めることで、最大の曲げ角度を決定できるようになります。またISO 7799 [15]では、シートの曲げや曲げ戻しを複数のサイクルで行う能力を評価できます。例えば最小曲げ半径を判定する手法には、標準化されていない試験がいくつか存在することもご承知おきください。
曲げ試験は車体製造に用いる材料の材料特性を確認する場合に有効です(図21)。ヘム加工では、シートの曲げやすさと曲げの限界について把握することが重要です。
図21: 曲げの外側で破損が見られる自動車製品のヘム接合部の断面図。出典: [16]
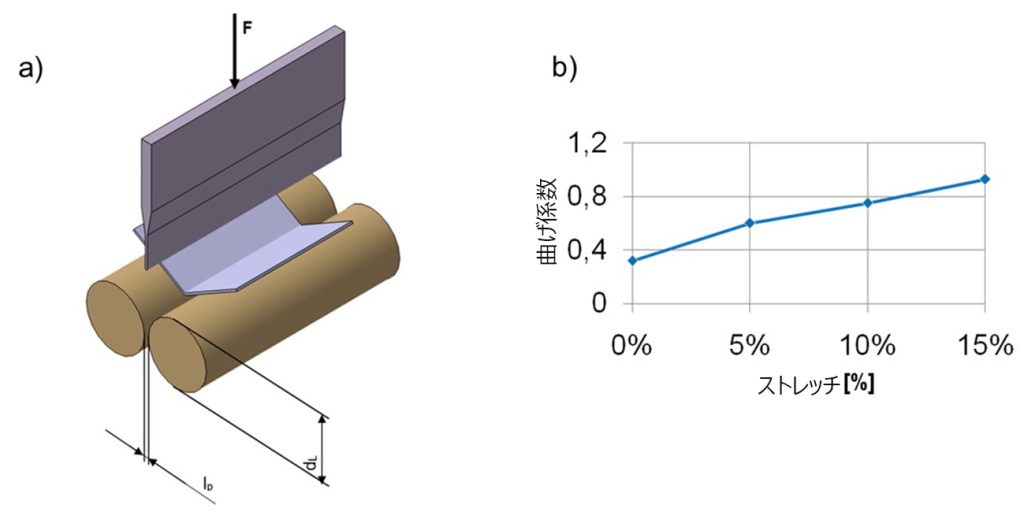
EN ISO 7438 [14]に記載された曲げ試験の装置には、ローラーと交換可能なパンチが必要となります(図21-a)。試験片はある角度に達するまで、あるいは曲げの限界に達するまで完全に曲げます。この試験では曲げ限界を評価できます。曲げの内半径と板厚の比から算出しますが、これは材料の曲げやすさを表しています。ヘミングの前にプレス成形されているため、変形度合いに応じた曲げ限界を算出できます(図21-b)。
図 21: a) DIN EN ISO 7348 に準じた曲げ装置。b) 変形度合いに対する曲げ限界のレベル。出典: [1].
試験の終了後、曲げた外側の表面を主観的な評価基準で評価し、品質等級を定義することもできます。測定した変数を定量的に記録することができないため、ここでは目視で確認します。それに応じた等級が決まり、そこから破損の限界を定義します(図22)。これ以降、等級2~3が破損の限界となるため、品質の観点からこれを超過することはできません。
図22: 曲げたエッジのサーフェス品質の等級。出典: [16]
機械的特性のばらつき
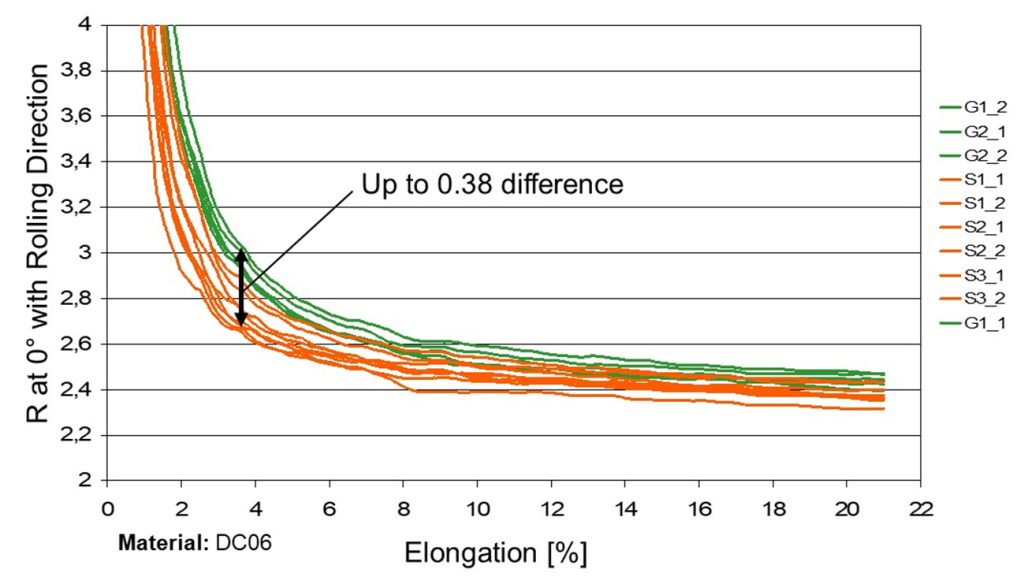
部品製造に使用するシートは、コイルの製造時から有する機械的特性にばらつきがあります。図23は、単一コイル内の冷間再圧延鋼板における異方性指数のばらつきを示しています。良品生産に必要な他の特性にも、すべてばらつきがあると考えられますが、このばらつきはプロセスが不安定になる要因となりえます。
図23:シートDC06の法線異方性のばらつき。出典: [1]
単体のシミュレーションモデルを使用すれば、部品の製造可能性を判断するための情報を得ることができます。しかし単体のシミュレーションではパラメータの自然発生的なばらつきを検討できないため、安定した製造プロセスは担保されません(図24)。
図24: 材料特性のばらつきを考慮せずに実行した単体シミュレーションの結果(右)と、実部品に生じた不具合(左)。出典: 著者
機械的特性だけでなく、ブランクホルダの荷重、トライボロジ(摩擦)、プレス速度などのプロセス係数にもばらつきは生じています。有限要素解析(FEA)ではこのようなばらつきを織り込んだ解析を実行できるため、機械的特性が最適な状態ではない場合でも、安定した生産を担保することが可能になります。
結論
生産活動のあらゆる状況において、材料の塑性挙動を正しく表現することは、これまで研究者を悩ませてきた課題です。本稿で紹介したさまざまな試験にはそれぞれ長所と短所があり、実際の現象にどれだけ類似しているかによって使い分ける必要があります。
確率論的なシミュレーションを実行するには、まず機械的特性に生じるばらつきを測定し、数学的に表現しなければなりません。確率論的なシミュレーションのモデルには、入力パラメータ(入力特性を含む)のばらつきがシミュレーション結果におよぼす影響を自動的に考慮させることができます。「現実世界のデジタルツイン」という考え方が浸透するにつれ、材料特性の正確な評価さらに重視されるようになっています。また、現実世界で自然に生じるばらつきを考慮する機能もいまや不可欠です。
プレス成形プロセスで活用するエンジニアリングのシステムには、精度と併せて「柔軟性」が求められています。システムから情報を取り出し、現実との比較を行い、再びシステムに戻す過程において、現実世界だけでなく、その機微までマッピングすることができれば、シナリオ分析やプロセスの自律的な是正を行うツールとしても活用することが可能になります。
ジョアン・エンリケ・コレア・デ・ソウザ 薄板プレス成形プロセスの分野にて、学術界および産業界の経験を有し、プレス成形およびチューブ成形、材料選択および最適化、プレス成形プロセスのシミュレーション、現場での成形性に関する諸問題の分析、迅速な金型製作、サーフェス・エンジニアリングなどのテーマに取り組んでいます。
参考文献
[1] Liewald M. Vorlesungsskript Werkstoffkundliche Grundlagen der Blechumformung. 2009, Institut für Umformtechnik, Universität Stuttgart.
[2] ISO12004-1:2020 Metallic materials — Determination of forming-limit curves for sheet and strip — Part 1: Measurement and application of forming-limit diagrams in the press shop.
[3] ISO12004-2:2021 Metallic materials — Determination of forming-limit curves for sheet and strip — Part 2: Determination of forming-limit curves in the laboratory.
[4] ISO 6892-1:2019 Metallic materials — Tensile testing
[5] Rozzo B, Deluca P, Rendina R. A new method for the prediction of formability limits in metal sheets. 1972, Sheet Metal Forming and Formability: Proceedings of the 7th biennial Conference of the IDDRG – International Deep Drawing Research Group.
[6] Sachs G. Ein neues Prüfgerät für Tiefziehbleche. 1930, Metallwirtschaft 9, 213.
[7] Pawelski O. 1967 Archiv für das Eisenhüttenwesen 38 (6), 437-42.
[8] DIN 50106, 2016 – Testing of metallic materials – Compression test at room temperature.
[9] Brosius A, Yin Q, Güner A, Tekkaya AE. A New Shear Test for Sheet Metal Characterization. 2010, Steel Research International 82 (4), 323-328.
[10] Hill RC. A theory of the plastic bulging of a metal diaphragm by lateral pressure. 1950, Lond. Edinb. Dublin Philos. Mag. J. Sci., 41 (322), 1133-1142.
[11] Nakazima K, Kikuma T, Hasuka K. Study on the formability of steel sheets. 1968, Yamata Technical Report, vol. 264, pp.141-154.
[12] Marciniak Z, Kuczynski K. Limit strains in the processes of stretch-forming sheet metal. 1967, Int. J. of Mechanical Sciences 9 (9), 613-620.
[13] ISO 16842, 2021 – Metallic materials — Sheet and strip — Biaxial tensile testing method using a cruciform test piece.
[14] EN ISO 7438, 2020 – Metallic materials. Bend test.
[15] ISO 7799:2000 Metallic materials. Sheet and strip 3 mm thick or less. Reverse bend test.
[16] Heyvaert S. Überprüfung der Bördelfahigkeit. 2006, Gesellschäftspräsentation Corus Aliminium Duffel, Belgium.


















![[ユーザー様向け]AutoForm-Sigmaを使用した量産ばらつき検討における効率的な設定のヒント](https://japanforming.com/wp-content/uploads/2022/06/107-量産ばらつき-cover-0-100x70.jpg)