コストを節減するために、生産に影響なくブランク・サイズを縮小できますか。

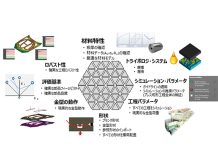
プレス成形業界では、材料およびコストを節減するために、ブランク・サイズを必要最低限まで縮小することが広く行われています。
エンジニアリング段階で検討するほか、一般的には、金型トライアウトの最終段階または部品製造の開始時に行います。
この最適化によって、年間数百万ユーロもの節減が可能となりますが、しかし必ず成功すると断言できるでしょうか。またブランク・サイズを最小化することで、部品製造に及ぼす悪影響が見落とされていないでしょうか。
もちろん、何らかの影響は避けられませんが、問題は、それを許容できるか否かです。つまり、実際には総合的にコストを削減できているか、ということです。
そのためにも、実際の影響を検証することが重要になります。

ブランク・サイズの縮小が生産の安定性に与える影響の詳細な分析は、正に自動車部品メーカーの技術部門が切望していたことです。
それを念頭に、どこから検討を開始すべきでしょうか。ブランク最適化の効果を特定するには、どのパラメータが必要で、どの結果変数を確認すべきでしょうか。

すでに述べたように、正確な材料特性(板厚や降伏応力など)を有するブランクを使う金型トライアウトにて、ブランクの最適化を行います。 その際には、このシナリオが生産シナリオを100%反映しているかを留意すべきですが、その答えはノーです。生産に使用する材料は一定範囲の特性を備えていますが、しかし複数の異なるコイル(各特性の値分布を確認してください)から生産するため、潤滑油、1分間のストローク数、プレス・タイプ、ブランクの位置などにばらつきが生じます。

部品製造工程の結果を事前にシミュレーションするには、まずロバスト性確認を実行し、特性のばらつきを考慮することが重要です。これで工程パラメータの変動幅を考慮する場合にも、適切な結果が得られます。つまり、ロバスト性確認を実行することで、生産中にコントロールできない変数のノイズを考慮できるようになります。以下の例では、次を検討します。

• • 潤滑
  • バインダ荷重
  • シート板厚
  • 材料の平均r値(材料異方性)
  • 材料降伏応力および引張強度(相関係数による相互依存)

例: ドア・インナー
ドア・インナー(1つの金型で2つの部品を製造)を例に、スプリングバックを含む製造の全工程を検討します。次のパラメータを評価基準とします。

1. 1. 1. 価格: ネストしたブランクの最低価格。
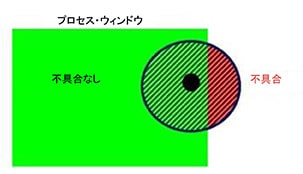
      2. 流入: D-30ドロー工程の後、ブランク・エッジはインナー・ドロービードを超えて流入してはいけません(ビードの中心線から4mm以上の距離 – 図1の黄色のライン)。
      3. われ不良率:マックス・フェイラーの最大値を1に設定し結果を確認することで、D-30最後の生産中のわれによる不良率を推測します。現在の基準結果は最大0.946と同等なため、要件を満たします。
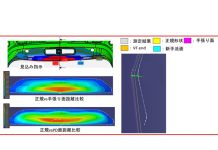
      4. スプリングバックの安定性: 最終部品のスプリングバック公差=±0.5mm

もちろん品質条件を追加することもできますが、この記事ではコンセプトをできるだけシンプルにします。ブランク修正では、基準ブランクの3方向すべて(対称と想定)の流入は、すでにインナー・ドロービードに非常に接近しています(図1を参照)。修正すると上記の条件#2に違反するおそれがあるため、ブランクの幅(1300mm)は一定でなければなりません。ただし、上下の2つのコーナーで、x方向でブランク・サイズを最小化できる可能性があります(図1を参照)。 よって、このシミュレーションでは、ロバスト性の設定として、両方のポイントを稼働幅が±30mmでx方向に相互依存した設計変数(つまりコントロール可能)として定義します。こうすることで、AutoForm-Sigma解析で複数のブランク・サイズのロバスト性を同時に評価できます。

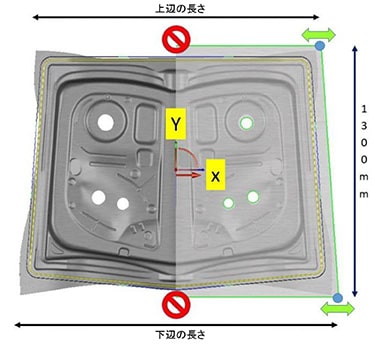
では、結果を検討しましょう。

結果：最適なブランク・サイズを決定する前に、まず設計上のロバスト性を検討します。
基準ブランク：ブランク・サイズ: 1500mm x 1680mm (上辺 x 下辺)

基準ブランクのロバスト性解析の結果、次の出力が得られます。

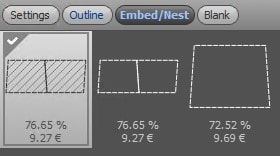
1. 1. 1. 価格: 9.27ユーロ (図2)
      2. D-30最後の流入: 満たす(図1)
      3. D-30最後のわれ不良率: > 10.7% (生産パラメータ変動幅に基づくマックス・フェイラー変動幅: 0.727 – 1.2)。注: 基準シミュレーションで、基準ブランクがこの限界を満たしています。ただし、ロバスト性を確認すると、この不良率の原因となりうるノイズ変数に敏感な領域があることがわかります(図3)。これは、金型トライアウトまたは生産において、材料またはその他のノイズ・パラメータが設計上の基準シミュレーションと異なる場合、われが発生する可能性があることを意味します。
      4. 最終部品のスプリングバックの安定性:不良率が0.007%以上の小さく局部的なオレンジ色の領域(Unreliable)以外、スプリングバック挙動は非常に安定しています(図4)。

最適化されたブランク：可能な入出力の組み合わせの計算が完了したら、結果を比較することができ、上記の条件に適合したより小さなブランク・サイズを検討できます。
　・新規のブランク・サイズ: 1525mm x 1633mm(上辺 x 下辺)

最適化したブランクのロバスト性解析の結果は、次の通りです。

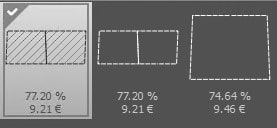
1. 1. 価格: 9.21ユーロ (図5)は、基準ブランクからブランクあたり0.6ユーロの削減
   2. D-30最後の流入制限: 満たす
   3. D-30最後のわれ不良率: > 3.1% (生産パラメータ変動幅によるマックス・フェイラー変動幅: 0.66 – 1.118)
   4. 最終部品のスプリングバックの安定性: 不良率が0.3%以上の小さな局部的なオレンジ色の領域(Min  Unreliable)以外、スプリングバック挙動は非常に安定しています(図6)

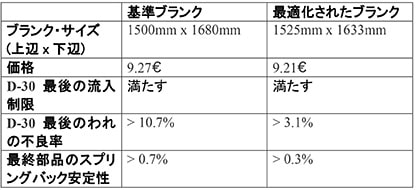
結論：表1に示した通り、生産に悪影響を与えることなく(同じ安定性で)、ブランク・サイズを縮小してコストを抑えることが可能です。最適化したブランクのスプリングバック挙動が同じ程度に安定していると、われの不良率は低くなります(つまり生産で不良品の割合が減るため、より大幅な節減を実現できます)。また、初期設計のブランク・サイズと比較すると、ブランクあたりの節減は0.06ユーロとなります。では結論として、このアプローチを採用する価値があるでしょうか。この事例に関しては、その価値は明白です。

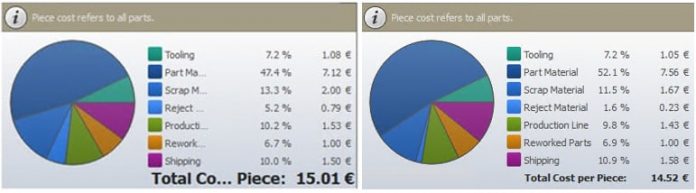
節減の合計額をより正確に推測するには、一定の生産量の部品コストを考慮する必要があります。生産量を200万個(自動車のライフサイクル)とすると、図7のように、部品あたり0.49ユーロの節減になります。ライフサイクル全体の節減額は980,000ユーロです。エンジニアリング段階にて実行する数時間のシミュレーションとしては、非常に高い投資利益率です。
さらに、工程がより安定すれば、生産を中断して、進捗に合わせて工程パラメータを調整する回数も減ります。金型ラインの不稼働期間は生産コストに大きく関係するため、この問題については、今後の記事で検討します。

ここで、次の質問について考えてみてください。コストを節減するためにブランク・サイズを縮小しても、部分的にでも工程に悪影響を及ぼすことはないと断言できますか? 無論、できません。プロジェクトをそれぞれ包括的に評価する必要があります。しかし、このような解析を実行することで、設計者は有意義な意思決定を行うことができるだけでなく、金型トライアウトや生産にて想定外の問題を回避できる可能性もあります。