きわめて正確なプロセス・シミュレーションを導く進路が示されます

オートフォーム社が導入したパレートの法則は、プレス成形シミュレーションの飛躍的な正確度向上の実現に向けて、業界の意識改革を促進するものです。このバート・カーレア博士(オートフォーム社テクニカル・ディレクタ)による連載記事では、プレス成形シミュレーションに導入されたAutoFormパレートの法則について紹介します。この法則をご理解いただくことで、プレス成形シミュレーションの正確度を効率的に高めることができます。

シミュレーションにおけるパレートの法則

パレートの法則では「80%の結果は20%の原因から生じる」と明言されています。経営コンサルタントのジョセフ・M・ジュランが、品質管理および品質改善の分野にこの法則を適用しました。イタリアの経済学者ヴィルフレド・パレートに因んで命名されたこの80:20の法則は、パレート分布とも呼ばれ、数学的にはベキ分布で表します。このベキ分布はパラメータ群に対して有効であるため、部品のプレス成形シミュレーションの設定にも適用できることは、想像に難くないでしょう。事実、数多くの自然現象がこの法則に準じていることが証明されています。

たとえばコンピュータ・サイエンスでは、パレートの法則は最適化に応用することができます。かつてマイクロソフト社では、報告されたシステム不具合の上位20%は、関連するエラーやクラッシュが発生する原因の80%を占めていることに着目しました。この上位20%の不具合をすべて修正すると、80%のエラーが解消したのです。このようにマイクロソフト社は、顕著な不具合を先に解消すべきことを学びました。

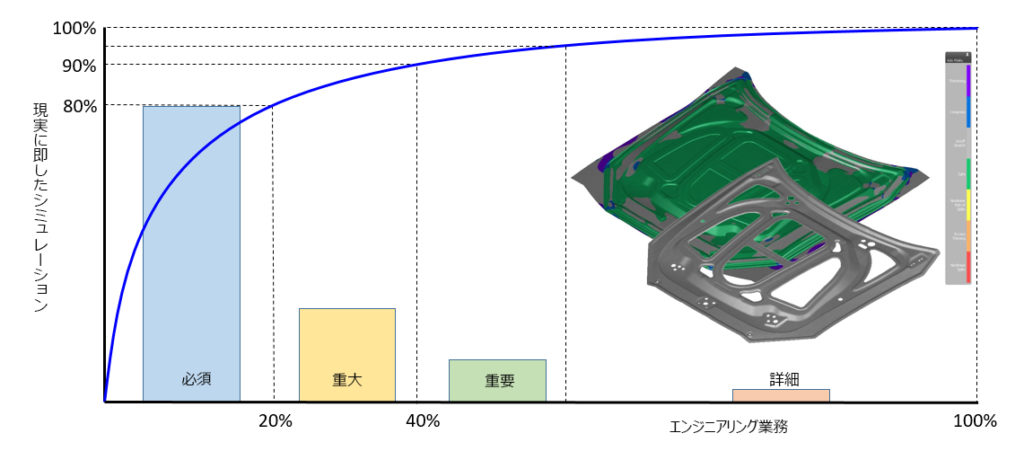
AutoFormパレートの法則の図表が示す通り、この法則はシミュレーションの正確度向上にも適用できます。最初に、正確なシミュレーション結果を得る上で不可欠な必須のインプット・パラメータ(シミュレーション結果に最も寄与するパラメータ)を特定します。そしてこれらの必須パラメータを集中的に定義して、検証を行います。すると金型製造現場における「未来の現実」の80％を表すシミュレーションの基礎が形成されます。

図1: シミュレーションのインプット・パラメータとシミュレーション結果に対する影響

すべての必須パラメータをコントロールできるようにすることが、正確なシミュレーション結果を得るための基盤となります。そしてパレートの法則に準じて、次のパラメータ群の検討を始めます。

このインプット・パラメータのグループは、重大パラメータと呼ばれるもので、全体の正確度には貢献しますが、最初のグループである必須パラメータほどの大きな影響はありません。優先順位を理解した上で、後続のパラメータを積み上げていくことで、シミュレーションの精度を高めていくことができます。しかし、優先順位を考慮する中で、最終的な正確度にほとんど貢献しないパラメータも見極めなければなりません。結局のところ、シミュレーション結果に大きく寄与するパラメータが確定せず、検証もされなければ、影響がほとんどない部分の微調整に時間を割くことに意味はありません。また、影響が大きい部分を無視して後回しにすることも、正確度指標のコンセプトに相反します。

つまりAutoFormパレートの法則は、さまざまなパラメータがシミュレーション結果にあたえる影響を見極める指針となるだけでなく、重要度の高いインプット・パラメータから低いものへと順を追って作業を進める、エンジニアリング・ベースのモデル構築プロセスを提案します。このように、この法則は一貫性のある正確なシミュレーション・モデルの分析的な構築を促進します。

AutoFormパレートの法則をプロセスおよびシミュレーションの成熟度に適用

フィージビリティの検討やプロセス・デザインの初期段階では、「既知」と「未知」の両方が存在します。開発チェーンの中で、部品パラメータは徐々に具体化され、定義されていくため、プロセスの成熟度と併せてシミュレーションの成熟度も高まるという観点から、パレートの法則では部品パラメータも検討します。

パレートの法則を図表化すると，エンジニアリング・パラメータのデータ入力は、4つのグループに分類されます。特に必須パラメータ、重大パラメータ、重要パラメータ、詳細パラメータは、正しい順番で入力しなければなりません。パレートの法則の基礎的な考え方では、わずか20%のパラメータ(必須パラメータに分類)がシミュレーション全体の正確度の約80%に貢献します。さらにパレートの法則では、後続のパラメータも全体の正確度に貢献しますが、全体的な正確度に対する貢献の度合いは低くなります。

重要度が高いパラメータが未検証の状態では、重要度が低いパラメータに多くの時間を費やすことが無意味であることも示しています。

これをプレス成形プロセスの開発チェーンに組み込むと、正確度の性質を検討する上で、複数の(代表的な)マイルストーンを明確に特定することができます。

特に初期の段階では、テーマの選択が達成目標となります。ここでは、基本的なスタイリングと初期のCAD形状のみが明らかです。そのため主に部品の形状と機能を検討します。詳細なプロセスの定義が存在しないため、部品のフィージビリティを中心にエンジニアリングを行います。

初期のマイルストーンは、部品設計のフリーズとなります。この段階のエンジニアリングでは、部品のフィージビリティのみならず、部品の製造可能性やプロセスのフィージビリティについて、より重点的に検討を重ねます。材料の仕様などの詳細を追加し、プレス機の選定やプレス工場の決定を行います。部品製造に必要な工程数を決定し、工程に工程ユニットを割り当てます。

金型設計および3Dモデルの構築は同時に行います。金型の外観を決定すると、3D金型設計データが完成します。シミュレーションの設定では、金型に作用する荷重を考慮します。

次の重要なマイルストーンは、切削へのデータリリースです。この時点では、すべての製造データが決定されていなければなりません。成形およびプレス成形のプロセスをすべて定義し、検証を完了してから、データをリリースします。ここで、仮想世界から現実世界に移行して、金型製造が開始します。

最後になりますが、今まで行ってきたエンジニアリングの良し悪しがはっきりわかるのは、金型トライアウトの段階であり、数ヶ月前に決定したエンジニアリング・コンセプトの成果を確認することになります。エンジニアリングした通りに現場が進んでいることが確認できれば、それはシステム全体が機能しているということです。

このように、パレートの法則のレンズを通して見ると、この開発チェーンの中で、より多くの部分が次々と具体化および定義され、プロセスの定義に反映されてゆくことがわかります。プロセスの定義を成熟させることは、シミュレーション・モデルを成熟させることと同等の関係にあります。シミュレーションに裏付けされた意思決定が行われるにつれてプロセスの成熟が進み、未来の現実がより正確にシミュレーションに反映されるようになり、すなわち正確度がより一層高まります。そして現場の結果がシミュレーション結果と一致したときに、究極の正確度に到達します。

プロセス・チェーンの意味するところは、エンジニアリングされた仮想のプロセスを、現実のプロセスにて忠実に再現することにあります。金型トライアウトおよび部品製造を円滑に行うために、エンジニアリングに労力を捧げるのです。

パレートの法則を図表化することで、把握している情報から正確な結果を得るために何をすべきかが明確になります。初期段階では把握できる情報がほとんどありませんが、そのような状況でも、その時点での「最善」を実現することが求められます。デジタル開発のあらゆる段階において、その状況に応じた「最善」が求められるのです。この連載では、この点について詳細に説明していきます。

プロセス・チェーンに沿ったある時点において、どれだけのデータが利用できるかを考慮しなければなりません。何を把握でき、何がすでに定義されていて、今後どのような意思決定を行うのでしょうか。この時点では、どのような前提条件を設定しなければならないのでしょうか。また、成熟している正確度において、どのレベルにどの部分が貢献するかも、パレートの法則は明らかに示しています。初期段階では、詳細にこだわることに意味はなく、最終的に、全体の正確度にはほとんど貢献しません。パレートの法則の図表から、そのような詳細は全体の正確度に5%しか寄与しないことがわかります。また細部にこだわることで全体像が見えなくなり、集中力や時間、お金、労力のロスにつながることもあります。

それと同時に、前提条件の設定やモデル化の際には、シミュレーションに適用するすべての定義が現実に変換できるようにしなければなりません。目指すべき目標は、抽象的な数値を作成することではなく、後段階の現実世界、つまり金型製造工場において、現実のモデル・ツインを作成することです。

本稿のポイントは、プレス成形プロセス・チェーンに沿って(最大の)正確性を目指すということです。そして、以下の点を考慮することが重要です。

• 各時点におけるプロセス・データの利用可能性
• どの入力値が最終結果の正確度にどの程度貢献するか
• 入力値の定義の論理的な順序 – 必須(最初)から詳細(最後)まで
• シミュレーション・モデルの定義をどのように現実に変換できるか

次回以降の連載では、AutoFormパレートの法則の適用について、さらに詳細に検討していきます。次回もお楽しみに。